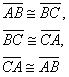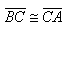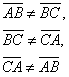Bloque I
Utilizas ángulos, triángulos y relaciones métricas.

Ángulos:

• Por su abertura
• Por la posición entre dos rectas paralelas y una secante ( transversal).
• Por la suma de sus medidas:
• Complementarios
• Suplementarios

 

Bloque II.

Comprendes la congruencia de triángulos

 

• Criterios de congruencia.

L,L,L (Lado, Lado, Lado)

L,A,L (Lado, Angulo, Lado)

 

A,L,A (Ángulo, Lado, Ángulo)

 

 

Bloque III.

Resuelve problemas de semejanza de triángulos y teorema de Pitágoras.

 

• Criterios de semejanza

*L,L,L

*L,A,L

*A,L,A

 

• Análisis y utilización del Teorema de Tales
• Análisis y utilización del  Teorema de Pitágoras.

 

 

Ángulos y su clasificación

 

Un ángulo se forma cuando dos líneas rectas se unen. La amplitud del giro de un ángulo se puede medir, y la unidad que se utiliza para expresarlo se llama grado. Si se realiza una vuelta completa, el ángulo mide 360 grados, escrito esto como 360°.		Media vuelta completa (lo que significa pasar justo al lado opuesto) es un giro de 180°. Este tipo de ángulo se llama ángulo llano.
Un cuarto de vuelta es un giro de 90°, también llamado ángulo recto.		Si un ángulo tiene menos de 90°, se llama ángulo agudo.
Si un ángulo tiene más de 90°, pero menos de 180°, se llama ángulo obtuso.		Si un ángulo mide más de 180°, se llama ángulo cóncavo.
Si un ángulo tiene menos de 180°, se llama ángulo convexo.		Si un ángulo tiene 0°, se llama ángulo nulo.

 

teoremas de los ángulos.

Teorema I: Dos ángulos adyacentes son suplementarios.

Teorema II: Los ángulos opuestos por el vértice son iguales.

Teorema III: Los ángulos consecutivos formados a un lado de una recta, suman 180°.

Teorema IV: La suma de los ángulos consecutivos alrededor de un punto, suman 360°.

Teorema V: Toda secante forma con dos paralelas ángulos alternos internos iguales.

Teorema VI: Toda secante forma con dos paralelas ángulos alternos externos iguales.

Teorema VII: Dos ángulos conjugados internos, entre paralelas, son suplementarios.

Teorema VIII: Los ángulos conjugados externos, entre paralelas, son suplementarios.

Teorema IX: Dos ángulos que tienen sus lados respectivamente paralelos y dirigidos en el mismo sentido, son iguales.

Teorema X: Dos ángulos que tienen sus lados respectivamente paralelos y dirigidos en sentido contrario, son iguales.

Teorema XI: Si dos ángulos tienen sus lados respectivamente paralelos, dos de ellos dirigidos en el mismo sentido, y los otros dos en sentido contrario, dichos ángulos son suplementarios.

Teorema XII: Dos ángulos agudos cuyos lados son respectivamente perpendiculares, son iguales.

Teorema XIII: Dos ángulos, uno agudo y otro obtuso, que tienen sus lados respectivamente perpendiculares son suplementarios.

Teorema XIV: Dos ángulos obtusos que tienen sus lados respectivamente perpendiculares, son iguales.

 

Teoremas sobre rectas paralelas

TEOREMA 5.1
Si dos rectas se cortan por una transversal y un par de angulos correspondientes son congruentes, entonces las rectas son paralelas.

TEOREMA 5.2
Si dos rectas se cortan por una transversal y un par de angulos alternos interiores son congruentes, entonces las rectas son paralelas.

TEOREMA 5.3
Si dos rectas se cortan por una transversal y un par de angulos alternos exteriores son congruentes, entonces las rectas son paralelas.

TEOREMA 5.4 
Si dos rectas se cortan por una transversal y un par de angulos interiores en el mismo lado de la transversal son suplementarios, entonces las rectas son paralelas.

TEOREMA 5.5
Dadas las rectas p, q y r, si p es paralela a q y q es paralela a r, entonces p es paralela a r.
TEOREMA 5.6
Si dos rectas paralelas se cortan por una transversal, entonces los angulos alternos interiores son congruentes.

TEOREMA 5.7
Si dos rectas paralelas se cortan por una transversal, entonces los angulos alternos exteriores son congruentes.

TEOREMA 5.8
Si dos rectas se cortan por una transversal, entonces los angulos correspondientes son congruentes.

TEOREMA 5.9
Si dos rectas paralelas se cortan por una transversal, entonces los angulos interiores del mismo lado de la transversal son suplementarios. 

• Fracciones

Teoremas en triángulos

Teorema 1: Relación entre lados

En todo triángulo cada lado es menor que la suma de los otros dos.

 

 

 

Teorema 2: Relación entre ángulos

 

En todo triángulo la suma de sus ángulos (interiores) es igual a 180°.

 

Teorema 3: Teorema de Pitágoras

En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

 

 

Clasificación de Triángulos

 

Los triángulos se pueden clasificar según la medida de sus lados o según la medida de sus ángulos.

Clasificación de triángulos según la medida de sus lados

El perímetro de un triángulo se calcula como “la suma del largo de sus lados”.
El área de un triángulo se calcula como “su base por la altura divida en dos”.

Triángulo Equilátero

El triángulo equilátero es aquel que tiene todos sus lados de la misma medida, en donde:

Triángulo Isósceles

El triángulo isósceles es aquel que tiene sólo dos lados de igual medida.

Triángulo Escaleno

El triángulo escaleno es aquel que tiene todos sus lados de distinta medida.

Clasificación de triángulos según la medida de sus ángulos

 

Triángulo Acutángulo

El triángulo acutángulo es aquel que tiene todos sus ángulos agudos.

Triángulo Rectángulo

El triángulo rectángulo es aquel que tiene un ángulo recto (< CAB).

Triángulo Obtusángulo

El triángulo obtusángulo es aquel que tiene un ángulo obtuso, tal como se muestra a continuación:

 

 

Ejemplo :

 

La hipotenusa de un triángulo rectángulo mide 405.6 m y la proyección de un cateto sobre ella 60 m. Calcular:

Soluciones:

1 Los catetos.

2 La altura relativa a la hipotenusa.

3 El área del triángulo.

 

 

Teorema de triángulos congruentes.

La suma del grado de medida de los ángulos de un triangulo es 180.

Teorema 23

Si un triangulo es equiangular, entonces el grado de medida de cada ángulo es 60 grados.

Teorema 24

Si un triangulo es un triangulo recto, entonces los ángulos agudos son complementarios.

 Teorema 25

La congruencia de los triángulos es reflexiva, simétrica, y transitiva.

AAL

Si dos ángulos y un lado no incluido de un triangulo son congruentes a los lados correspondientes y al ladono incluido de otro triangulo, entonces los triángulos son congruentes.

Teorema del Triangulo Isósceles

Si dos lados de un triangulo son congruentes, entonces los ángulos opuestosa esos lados son congruentes.

Teorema 26

Si un triangulo es equilátero, entonces el triangulo es equiangular.

Teorema 27

Si un triangulo es equilátero, entonces cada ángulo tiene un grado de medida de 60 grados.

Teorema 28

Si dos ángulos de un triangulo son congruentes, entonces los lados opuestos a ese ángulo soncongruentes.

Teorema 29

Si un triangulo es equiangular, entonces el triangulo es equilátero.

AH

Si la hipotenusa y un ángulo agudo del triangulo recto son congruentes a la hipotenusa correspondiente y alángulo agudo de otro triangulo recto, entonces los triángulos son congruentes.

CC

Si los catetos de un triangulo recto son congruentes a los catetos correspondientes a otro triangulo recto,entonces los triángulos son congruentes.

CA

Si un lado y un ángulo agudo de un triangulo recto son congruentes a un lado correspondiente y a un ánguloagudo de otro triangulo recto, entonces los triángulos son congruentes.

“Inecualidades de los triángulos”Teorema del Angulo Exterior

Si un ángulo es un ángulo exterior del triangulo, entonces su medida es igual ala suma de las medidas de los dos ángulos interiores lejanos.

Teorema de la inecualidad

Por cualquier numero s y p, s>p si y solamente si existe un número positivo b talque s = p+b.

Teorema 30

Si un ángulo es un ángulo exterior de un triangulo, entonces su medida es mayor que la medida decualquier ángulo interior lejano.

Teorema 31

Si la medida de dos lados de un triangulo no son iguales, entonces la medida de los ángulosopuestos a esos lados no son iguales en el mismo orden.

 

Teorema de triángulos semejantes:



Dados los triángulos ABC y A'B'C' determinamos los lados y ángulos homólogos.

Lados homólogos:

a y a', b y b', c y c'

Ángulos homólogos:

Dos triángulos son semejantes cuando tienen sus ángulos homólogos iguales y sus lados homólogos proporcionales.

La razón de la proporción entre los lados de los triángulos se llama razón de semejanza.

La razón de los perímetros de los triángulos semejantes es igual a su razón de semejanza.

 

 

La razón de las áreas de los triángulos semejantes es igual al cuadrado de su razón de semejanza.

teoremas de triángulos semejantes.

1Dos triángulos son semejantes si tienen dos ángulos iguales.

 

 

2 Dos triángulos son semejantes si tienen los lados proporcionales.

 

 

3 Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.

 

 

 

Semejanza de triángulos rectángulos

1Dos triángulos rectángulos son semejantes si tienen un ángulo agudo igual.

2Dos triángulos rectángulos son semejantes si tienen los dos catetos proporcionales.

3Dos triángulos rectángulos son semejantes si tienen proporcionales la hipotenusa y un cateto.

Ejemplos prácticos

1. Determinar la altura de un edificio que proyecta una sombra de 6.5 m a la misma hora que un poste de 4.5 m de altura da una sombra de 0.90 m.

2.Los catetos de un triángulo rectángulo que miden 24 m y 10 m. ¿Cuánto medirán los catetos de un triángulo semejante al primero cuya hipotenusa mide 52 m?

 

teorema de Thales de Mileto.

Tales de Mileto.

Cuando en geometría hablemos del Teorema de Tales (o Thales), debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.

El primero de ellos se refiere a la construcción de un triángulo que sea semejante a otro existente (triángulos semejantes son los que tienen iguales ángulos).
Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos (los circuncentros se encuentran en el punto medio de su hipotenusa).

Primer teorema

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.
Entonces, veamos el primer Teorema de Tales en un triángulo:

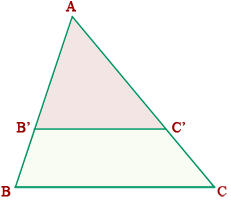Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC. Lo que se traduce en la fórmula

Ver: PSU: Geometría;
Pregunta 01_2005
Pregunta 05_2006
Hagamos un ejercicio como ejemplo:

En el triágulo de la derecha, hallar las medidas de los segmentos a y b. Apicamos la fórmula, y tenemos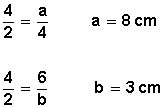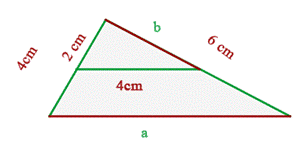

Como vemos, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario.

Corolario

Al establecer la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.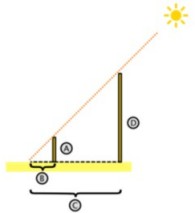

Una aplicación del Teorema de Tales.

Por ejemplo, en la figura de la izquierda se observan dos triángulos que, en virtud del Teorema de Tales, son semejantes. Entonces, como corolario, el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande.
En virtud del teorema de Tales, ambos triángulos son semejantes y se cumple que:

Este corolario es la base de la geometría descriptiva. Su utilidad es evidente; según Heródoto, el propio Tales empleó el corolario de su teorema para medir la altura de la  pirámide de Keops en Egipto.

La leyenda de Tales y las pirámides

Según la leyenda (relatada por Plutarco), Tales de Mileto en un viaje a Egipto, visitó las pirámides de Guiza (Keops, Kefrén y Micerinos), construidas varios siglos antes.
Admirado ante tan portentosos monumentos, quiso saber su altura.
La leyenda dice que solucionó el problema aprovechando la semejanza de triángulos (y bajo la suposición de que los rayos solares incidentes eran paralelos).
Así, estableció una relación de semejanza (Primer teorema de Tales) entre dos triángulos rectángulos, los que se grafican en la figura a la derecha.
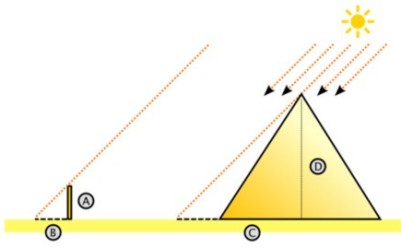Por un lado el que tiene por catetos (C y D) a la longitud de la sombra de la pirámide (C, conocible) y la longitud de su altura (D, desconocida), y por otro lado, valiéndose de una vara (clavada en el suelo de modo perfectamente vertical) otro cuyos catetos conocibles (A y B) son, la longitud de la vara (A) y la longitud de su sombra (B). Como en triángulos semejantes, se cumple que , por lo tanto la altura de la pirámide es , con lo cual resolvió el problema.

Otra variante del Teorema de Tales

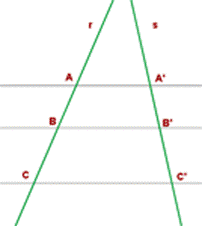Del primer teorema de Tales se deduce además lo siguiente (realmente es otra variante de dicho teorema, y, a su vez, consecuencia del mismo): Si dos rectas cualesquieras (r y s) se cortan por varias rectas paralelas (AA’, BB’, CC’) los segmentos determinados en una de las rectas (AB, BC) son proporcionales a los segmentos correspondientes en la otra (A’B’, B’C’).

 

TEOREMA DE PITÁGORAS

 

	En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. a2 + b2 = c2
Cada uno de los sumandos, representa el área de un cuadrado de lado, a, b, c. Con lo que la expresión anterior, en términos de áreas se expresa en la forma siguiente:
El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.